Ratio & Proportion - Things To Remember!

Types of Ratio


The different types of ratio are explained as under

  1. Duplicate Ratio If two numbers are in ratio, then the ratio of their squares is called duplicate ratio. If x and yare two numbers, then the duplicate ratio of x and y would be x2 : y2.

    2. Duplicate ratio of (x : y) is (x2 : y2).

    For example Duplicate ratio of 3 : 4 = 32 : 42 = 9 : 16

  2. Sub-duplicate Ratio If two numbers are in ratio, then the ratio of their square roots is called sub-duplicate ratio. If x and y are two numbers, then the sub-duplicate ratio of x and y would be (x : y)

    3. Sub-duplicate ratio of (x : y) is (x : y).

  3. Triplicate Ratio If two numbers are in ratio, then the ratio of their cubes is called triplicate ratio. If x and y are two numbers, then the triplicate ratio of x and y would be x3 : y3.

    4. Triplicate ratio of (x : y) is (x3 : y3).

    For example Triplicate ratio of 2 : 3 = 23 : 33 = 8 : 27

  4. Sub-triplicate Ratio If two numbers are in ratio, then the ratio of their cube roots is called sub-triplicate ratio. If a and b are two numbers, then the sub-triplicate ratio of a and b would be a1/3 : b1/3

    5. Sub-triplicate ratio of (a : b) is (a1/3 : b1/3).

    If a = c , then a + b = c + d .    
    b d a - b c - d

    [componendo and dividendo]

    For example Sub-triplicate ratio of 1 : 125 = (1)1/3 : (125)1/3 = 1: 5

  5. Inverse Ratio If two numbers are in ratio, then their antecedent and consequent are interchanged and the ratio obtained is called inverse ratio. If x and y are two numbers and their ratio is x : y,
    then its inverse ratio will be y : x

    6. For example Inverse ratio of 4 : 5 is 5 : 4.

  6. Compound Ratio If two or more ratios are given, then the antecedent of one is multiplied with antecedent of other and respective consequents are also multiplied with antecedent of other and respective consequents are also multiplied. If a : b, c : d and e : f are three ratios, then their compound ratio will be ace : pdf.

    7. The compounded ratio of the ratios: (a : b), (c : d), (e : f) is (ace : bdf).

    For example The compound ratio of 2 : 5, 6 : 7 and 9 : 13 = (2 x 6 x 9) / (5 x 7 x 13) = 108 / 455

MIND IT !

  1. If the antecedent is greater than the consequent, then the ratio is known as the ratio of greater inequality, such as 7 : 5.
  2. If the antecedent is less than the consequent, then the ratio is called the ratio of less inequality, such as 5 : 7.

Comparison of Ratios

We say that (a : b) > (c : d)     a > c .
b d

Rules used to compare different ratios are as follows


Rule #1: If the given ratios are a : b and c : d, then
(i) a : b > c : d, if ad > bc (ii) a : b < c : d, if ad < bc (iii) a : b = c : d, if ad = bc


Example 1: Which is grater 5/8 or 9/14 ?

sol. Let a/b = 5/8 and c/d = 9/14; 

ad = 5 x 14 = 70 and bc = 8 x 9 =72

Therefore  ad < bc

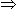  a/b < c/d = 5/8 < 9/14


Rule #2: If two ratios are given for comparison, convert each ratio in such a way that both ratios have same denominator, then compare their numerators, the fraction with greater numerator will be grater.


Example 2:Find the greater ratio between 2 : 3 and 4 : 5.

sol. (2 x 5) / (3 x 5) = 10/15 and
       (4 x 3) / (5 x 3) = 12/15

[ LCM of 2/3 and 4/5 i.e., 3 and 5 is 15]

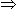12/15 > 10/15

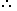  4 : 5 > 2 : 3


Rule #3: If two ratios are given for comparison, convert each ratio in such a way that both ratios have same numerator, then compare their denominators, the fraction with lesser denominator will be greater.


Example 3: Find the least fraction between 6/7 and 7/9.

sol. (6 x 7) / (7 x 7) = 42/49 and
       (7 x 6) / (9 x 6) = 42/54

[ LCM of 6/7 and 7/9 i.e., 6 and 7 is 42] 

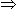 42/49 > 42/54
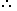 6/7 : 7/9

Proportion


An equality of two ratios is called the proportion. If a/b = c/d or a : b = c : d, then we can say that a, b, c and d are in proportion and can be written as a : b :: c : d, where symbol ' :: ' represents proportion and it is read as 'a is to b' as 'c is to d'.

Here, a and d are called 'Extremes' and b and c are called as 'Means'.

Product of means = Product of extremes.

Thus, a : b :: c : d (b x c) = (a x d).

Variations


We say that x is directly proportional to y, if x = ky for some constant k and we write, x 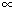y.

We say that x is inversely proportional to y, if xy = k for some constant k and

we write, x 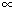1 .
y

Ready to Practice!