Height And Distance Aptitude Questions

Q 1 - The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:

Let AB be the wall and BC be the ladder.
Then, ∠ACB = 45° and AC = 7.5 m
AC/BC= Cos (45) =1/√2
BC=7.5√2

Q 2 - A vertical pole fixed to the ground is divided in the ratio 1:4 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 16 m away from the base of the pole, what is the height of the pole?

Let CB be the pole and point D divides it such that BD : DC = 1 : 4 = X:4X
Given that AB = 16 m
Let the the two parts subtend equal angles at point A such that
CAD = BAD = Θ
=>tan Θ=X/16 =>X=16 tan ( Θ) ------ (1)
=>tan( Θ+ Θ)=4X/16
=>16 tan (2 Θ)=4X
=>16(2tan ( Θ))/(1-tan ( Θ)2)=4X ------ (2)
From eqn 1 & 2 2X/(1-tan ( Θ)2)=4X (X=16tan Θ)
1/(1-(X/16)2)=2
1-(X/16)2=1/2=>162-
X2=162/2=>X2=128
=>X=8√2
=>Height of pole BC = X+4X=5X=40√2

Q 3 - From the top of mast head of height 210 meters of a ship, a boat is observed at an angle of depression of 30° then the distance between them is

From the right angled triangle CAB
Tan(30) =210/X
=>X=210/Tan(30)=210/(1/√3)=210√3

Q 4 - A step inclining toward a vertical divider makes a point of 45 with the even ground. The step's Foot is 3m from the divider. Find Length of the step?

Let AB be the step and BC be the divider and let AC be the even ground.
Then, ∠CAB=45 and AC=3m. Let AB= x Meter.
From right △ ACB, we have
AB/AC =sec. 45° = √2 => x/3 = √2
X= 3√2m = (3*1.41) m= 4.23m.
∴ Length of the stepping stool is 4.23 m

Q 5 - From The highest point of a 10 m high building, the edge of rise of the of the highest point of a tower is 60° and the despondency's edge of its foot is 45°,Find The tower's stature. (take√3=1.732)

Let AB be the building and CD be the tower.
Draw BE perpendicular to CD.
At that point CE =AB = 10m, ∠EBD= 60° and ∠ACB= ∠ CBE=45°
AC/AB= cot45°=1 = >AC/10 =1 => AC = 10m.
From △ EBD, we have
DE/BE= tan 60°=√3 => DE/AC= √3
=> DE/10= 1.732 =>DE = 17.3
Height of the tower = CD= CE+DE= (10+17.32) = 27.3 m.

Q 6 - A 10 m long stepping stool is put against a divider. It is slanted at a point of 30°to the ground. The separation of the stepping stool's foot from the divider is:

Let AB be the step slanted at 30°to the Ground AC.
Then, AB=10m and

Q 7 - A kite is flying at a tallness of 75 m from the level of ground, joined to a string slanted at 60° to the level. The string's length is:

Let AB be the kite and AC be the level ground
So that BC - AC.
At that point, ∠BAC=60°and BC=75m. Let AB=x meters.
Presently AB/BC=coses60°=2/ √3
=> x/75=2/√3 =>x=150/√3 =150* √3/3=50 √3m.
∴ Length of the string=50 √3m.

Q 8 - On the level plane, there is a vertical tower with a flagpole on its top. At a point 9m far from the tower, the edges of rise of the top and Base of the flagpole are 60°and 30°respectively.The flagpole's tallness is:

Let AB be the tower and BC be the flag pole and let O be the point of observation.
Then, A=9m, ∠AOB=30°and ∠AOC=60°
AB/OA=tan30°=1 ∠ =>AB/9=1∠
=>AB=(9*1/ √3* √3/√3)= 3 √3m.
AC/AO=tan60°=√3 =>AC/9= √3 =>AC= 9√3m.
∴BC= (AC-AB) = (9 √3-3 √3) m=6 √3m.
∴ Height of the flagpole is 6 √m.

Q9. Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:

Let AB be the lighthouse and C and D be the positions of the ships.

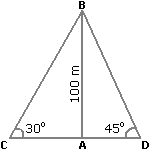
Then, AB = 100 m, ACB = 30° and ADB = 45°.

AB	= tan 30° =	1	AC = AB x 3 = 1003 m.
AC		3

AB	= tan 45° = 1 AD = AB = 100 m.
AD

CD = (AC + AD)	= (1003 + 100) m
	= 100(3 + 1)
	= (100 x 2.73) m
	= 273 m.

Q10 The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:

Let AB be the wall and BC be the ladder.

Then, ACB = 60° and AC = 4.6 m.

AC	= cos 60° =	1
BC	= cos 60° =	2

BC	= 2 x AC
	= (2 x 4.6) m
	= 9.2 m.